| Ratio |
|---|
| Comparing using ratio |
| Increasing ratios |
| Proportion |
| Sharing using ratio |
| Assessment questions |
Sh 200 was shared among Jane, Celine and Harriet in the ratio 2:3:5.
How much did each receive?

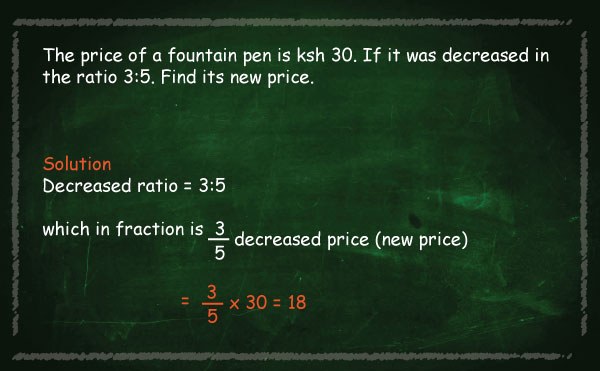
Ratios can have more than two numbers.
For example concrete is made by mixing cement, sand, stones and water.
A typical mix of cement, sand and stones is written as a ratio, such as 1:2:6.
You can multiply all values by the same amount and you will still have the same ratio.
So if you used 10 buckets of cement, you should use 20 of sand and 60 of stones.
Example: if you have just put 12 buckets of stones into a wheelbarrow, how much cement and how much sand should you add to make a 1:2:6 mix?
Let us lay it out in a table to make it clearer:
| cement | Sand | Stones | |
| Ratio needed | 1 | 2 | 6 |
| You have | 12 |
That is OK, you simply have twice as many stones as the number in the ratio ... so you need twice as much of everything to keep the ratio.You can see that you have 12 buckets of stones but the ratio says 6.
Here is the solution:
| cement | Sand | Stones | |
| Ratio needed | 1 | 2 | 6 |
| You have | 2 | 4 | 12 |
Why are they the same ratio? In the 1:2:6 ratio there is 3 times more Stones as Sand (6 vs 2), and in the 2:4:12 ratio there is also 3 times more Stones as Sand (12 vs 4) ... similarly there is twice as much Sand as Cement in both ratios.And the ratio 2:4:12 is the same as 1:2:6 (because they show the same relative sizes)
That is the good thing about ratios. You can make the amounts bigger or smaller and so long as the relative sizes are the same then the ratio is the same.