| Ratio |
|---|
| Comparing using ratio |
| Increasing ratios |
| Proportion |
| Sharing using ratio |
| Assessment questions |
- A ratio compares values.
- A ratio says how much of one thing there is compared to another thing.

- In the above image, there are 3 blue squares to 1 yellow square
1. To separate the value for example 3:1
2. Instead of the: you can use the word "to" for example 3 to 1
3. You can write it like a fraction i.e
- Ratio can be scaled up or increased
How many squares are blue and how many are yellow in the below image?
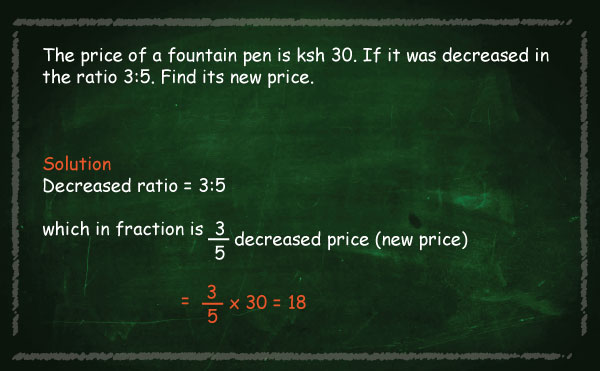
6:2
3:1
The ratio here is also 3 blue squares to 1 yellow square even though there are more squares.
When scaling ratios up or down the trick is always to multiply or divide the number by the same value.
For Example:
4 : 5 is the same as
4 x 2 : 5 x 2
This equals 8 : 10
For example to make pancakes you can use 3 cups of flour and 2 cups of milk.
If you need pancakes for more people you will need 4 times the quantity so you multiply the number by 4.
i.e
3 x 4 : 2 x 4
This equals 12 : 8
This ratio is still the same!
The examples given in the previous pages have been part to part i.e comparing one part to another part.
A Ratio can also show a part compared to the whole lot
For Example: There are 5 students, 2 are boys and 3 are girls.
The ratio of boys to girls is 2:3 or 2/3
The ratio of girls to boys is 3:2 or 3/2
Part to Whole
The Ratio of boys to all the students is 2:5 or 2/5.
The Ratio of girls to all the students is 3:5 or 3/5.
What is the ratio of:
3:1
1:3
3:4
1:4
A percent is a ratio whose second term is 100.
Percent means parts per hundred.
The word comes from the Latin phrase per centum, which means per hundred.
In maths the symbol % is used for percent.
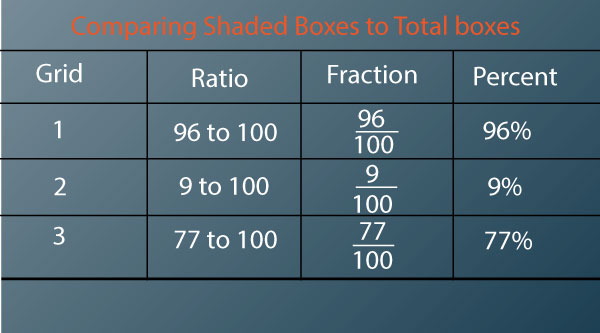
Look at the table below:
As stated earlier, ratios are typically written with a colon.
In our example, the ratio of boys to girls is 2:3.
The ratio can be converted to a fraction by replacing the colon with a fraction bar.
For example, 2:3 can be written as 2/3.
Divide the numerator (top number) by the denominator (bottom number) in your fraction.
In our example, if you divide 2/3, you get .666666
If necessary, round the decimal.
If your decimal goes on for several places, as our example does, you will need to round it.
Sometimes, you may be asked to round to a certain number of places.
If not, round to two decimal places. So, we would round our number to 0.67
Express your answer as a ratio.
So, the ratio of boys to girls in the class is 0.67.

1. To plaster a house, sand and cement were mixed in the ratio 5:1. If 24 bags of cement each weighing 50 kg were used, how much was the amount of sand used in tonnes?
A. 1.2 B. 6 C. 4.8 D. 60
2. Mumbua and Njeri each made a 20 kg mixture of maize and beans. Mumbua mixed the maize and beans in the ratio 3:2. Njeri mixed the maize and beans in the ratio 1:3. How many more kilograms of beans did Njeri use than Mumbua?
A. 15 B. 12 C. 8 D. 7
3. A blanket is made by joining 80 squares of 3 different colours; blue, green and yellow, in the ratio 2:3:5 respectively. One ball of wool is used to make four such squares. How many balls of green wool are used for one blanket?
A. 4 B. 6 C. 10 D. 20
4. A painter mixed blue and yellow powder so that their weights were in the ratio 3:2. The total weight of the mixture was 30 kg. What was the weight, in kilograms, of the yellow powder used?
A. 6 B. 12 C. 18 D. 20
5. There were 420 people attending a meeting. The ratio of men to women was 3:4. Later, 60 men and 40 women left the meeting. What was the ratio of men to women who remained?
A. 3:2 B. 3:5 C. 7:9 D. 6:7
6. The ratio of sheep to goats to cows is 3:5:2. There are 36 cows. What is the total number of goats and sheep?
A. 180 B. 144 C. 90 D. 54
7. The ratio of boys to girls in a school is 7:8. If there are 168 boys, how many pupils are there in the school altogether?
A. 360 B. 147 C. 192 D. 315
8. In her farm, Wambui had goats, sheep, and cows in the ratio 5:3:2. At the beginning, she had 50 animals but later sold some of them leaving her with 36. If the number of goats, sheep, and cows that remained were in the ratio 2:1:1, how many sheep did he sell?
A. 14 B. 6 C. 9 D. 15
9. A sum of money was shared between M’mukindia and Ntonyiri in the ratio 3:7. If Ntonyiri got sh 12 more than M’mukindia, how much did M’mukindia get?
A. Sh 30 B. Sh 21 C. Sh 18 D. Sh 9
10. In a school, the ratio of boys to girls is 3:2. There are 400 pupils in the school. during an athletics competition, of the girls took part. How many girls did not take part?
A. 140 B. 20 C. 210 D. 160
11. The ratio of the weights of two boys is 2:3. If the lighter boy weighs 36 kg, what is the difference in the weights of the two boys?
A. 18 kg B. 12 kg C. 54 kg D. 90 kg
12. Achieng and Cherono shared some money in the ratio 4:5 respectively. Cherono got sh 6 more than Achieng. How much money did Achieng get?
A. Sh 24 B. Sh 30 C. Sh 48 D. Sh 54
13. In Koome’s farm, the ratio of cows to goats is 5:3 while that of goats to sheep is 4:7. If he has 21 sheep, what is the total number of his animals?
A. 32 B. 33 C. 41 D. 53
14. The ratio of girls to boys in a school is 3:2. If there are 120 more girls than boys, how many boys are there in the school?
A. 600 B. 400 C. 360 D. 240