Whole numbers are called integers.
Examples of whole numbers are 2, 3, 7, 21 and 341.
A fraction is a part of an integer or a whole number. The image below tries to define a fraction as being a portion of a whole number. "a fraction of a the whole"

A Fraction is actually the quotient ratio form of two quantities.
Video on fractions
A fraction is expressed as:
A fraction can be simplified or reduced to a value when its numerator and denominator have no common factors.
Working with the fraction is easier when they're simplified. We work with fractions when we multiply, subtract add or divide.
An equivalent fraction where the numerator and denominator have no common factors is used to simplify the fraction.


Simplify `56/64`
``
Simplify`24/36`
1. Proper fractions: where the numerator is less the denominator for example
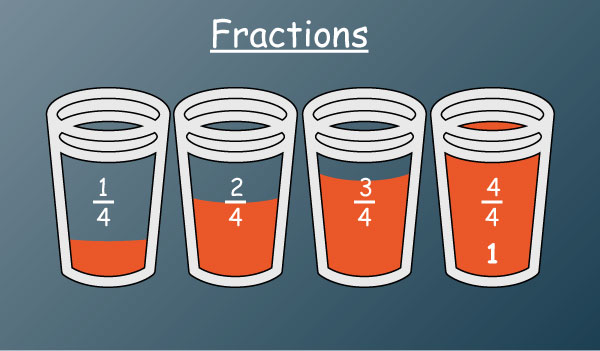
2. Improper fractions: where the numerator is greater than the denominator for example
3. Mixed number fractions as called mixed numbers: consists of a whole number and a proper fraction e.g.



[resource: 977, align: left]
To convert mixed fractions to improper fractions follow the following steps;
Step 1: multiply the denominator with the whole number
Step 2: add the numerator to the product of step 1 to get the new numerator
Step 3: The denominator of the remains the same.

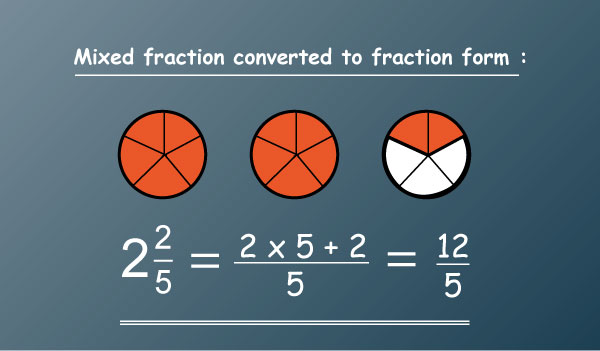


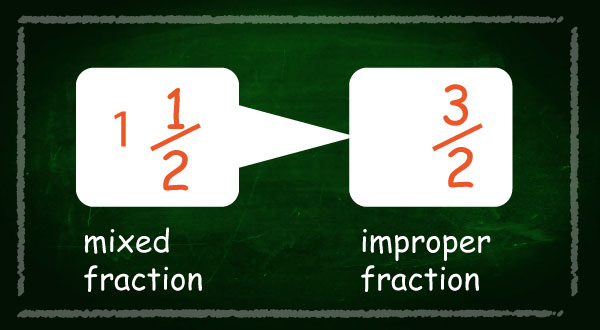
To convert improper fractions to mixed fractions follow the steps below;
Step 1: divide the numerator with the denominator,
Step 2: add the quotient is whole number and the remainder is the new numerator while the denominator remains the same
