| Volume & Capacity |
|---|
| Assessment Questions |
The car can fit inside the container since there is Space
The amount of space occupied by an object is called its volume.
To measure volume we can use the following units:
The amount that a container can hold is called capacity.
[resource: 2282, align: left]
The glass in the above image can hold a certain amount of liquid. This is called capacity.
Capacity can be measured using the units:
Relationships involving units of volume and capacity are given below.
Volume
1 000 000 cm³ = 1m³
Capacity
100 ml = 1 dl
10 dl = 1 l
1 000 ml = 1 l
Volume and capacity
1 cm³ = 1 ml
1 000 cm³ = 1
l 100 cm³= 1 dl
1 m³ = 1 000 l
Conversion and basic operations involving units of volume and capacity can be worked out using the relations given above.
To obtain the volume of cubes and cuboids, we can use the number of layers in a stack or apply formulae.
We can also use the relevant formulae to work out the volume of cylinders and solids with uniform cross-sections such as a triangular prism.
A cube has 6 surfaces each of which is a square or all its edges (length, width and height) are
of the same length.
The volume is obtained by multiplying the 3 dimensions:
This is a Cuboid.
It has 6 faces which are not equal.
The opposite faces are equal to each other.
Volume of a cuboid = base area x height
Hence, ` l x w x h`
V = l × w × h
A Cylinder has a Top, Base and a Curved Surface.
Area of the base is the area of a circle = πr^2
Volume= Area of the base x Height
Play this video to see how to find the Volume of a Cube
Play this video to see how to find the Volume of a Cylinder
When we have cylinder , cube and cuboid together to form an object we call it a combined shape.
Work out the volume of the below solid (Take π = 22 / 7)
The length, width, and height of the cuboid are 15 m, 7 m, and 8 m, respectively.
Also, the diameter of the half-cylinder is 7 m and its height is 15 m.
So, the required volume = volume of the cuboid + 1/2 volume of the cylinder
Work out the volume of the below solid (Take π = 22 / 7)

This solid is made up of a cuboid with a cylindrical hole.
To get its volume, get the volume of the cuboid (l x w x h) and Get the volume of the cylinder (pie x r x r x h)
Subtract the volume of the cylinder from the volume of the cuboid
Volume of the Cuboid = 16.2cm x 16.6cm x 24cm
= 6298.56cm cubed
Volume of the Cylinder = ` `
= 925cm cubed
Volume of the solid is therefore:
= (6298.56 - 924)cm cubed
= 5374.56 cm cubed.
The bottom of a rectangular trough measures 150 cm by 350 cm.
If the height of the trough is 200 cm find its:
(a) volume in m³
(b) capacity in litres.
Example 2
A cylinder has a height of 200 cm. Its base radius is 50 cm.
Calculate its volume in m³. (Take ? = 3.14).
Example 3
A triangular prism has a volume of 360 cm³.
The prism has a length of 15 cm and the height of its triangular face is 8 cm.
Calculate the base of the triangular face.
Example 1
(a) Volume = length x width x height
= 150 cm x 350 cm x 200 cm
= 10 500 000 cm³
1 000 000 cm³ = 1 m³
Volume in m³
= 10 500 000 / 1 000 000
= 10.5 m³
(b) Capacity: 1 000 cm³ = 1 l
10 500 000 cm³ = l0 500 000/1 000 l
= 10 500 l
Solution
Volume = pie r² h
= (3.14 x 50 x 50 x 200) cm³
= 1 570 000 cm³
1 000 000 cm³ = 1 m³
Volume = 1 570 000 / 1 000 000 (m³)
= 1.57 m³
Solution
Let b represent the base of triangular face.
Volume = Area of cross-section x length
= Area of the triangular face x length
360 =1/2 x b x 8 x 15
b x 8 x 15 = 2 x 360
b = 2 x 360 / 8 x 15
= 6cm
The amount of liquid or gas that a container will hold when full. Or the volume of liquid that can fit inside the container
It measured in milliliters (ml), litre(l), deciliters(dl).
The standard unit used for capacity is litre (l).
Watch this video
Look at this too!
A cube with a volume of 1 cm3 will hold 1 ml of liquid
I ml = 1 cm3
1L = 1000 ml = 1000 cm3
.
The tank on a fuel tanker is in the shape of a cylinder 10 meters long, with a diameter of 3 metres.
a) Find to 2 decimal places the volume of the tank in cubic meters.
b) How many litres of fuel can this tank hold?
Volume =πr^2h
Take pie as 3.14
3.14×1.5×1.5×10
= 70.65m3
1M3= 1000L
70.65M3= ?
` `
= 70,650L
Class 8
1. What is the difference in volume of a cube whose sides measure 7 cm and a cylinder whose height 7 cm and the diameter of the base is 7 cm? (Take 22/7)
A. 73.5 cm3 B. 343 cm3 C. 269.5 cm3 D. 0 cm3
2. The figure below shows a semi-circular water container 3 m long. The diameter of the semi-circle is 1.4 m.
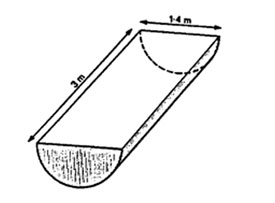
What is the volume of the container in cubic metres? (Take )
A. 4.41 B. 4.62 C. 2.31 D. 23.1
3. Amjit made a hollow block as shown in the diagram below.
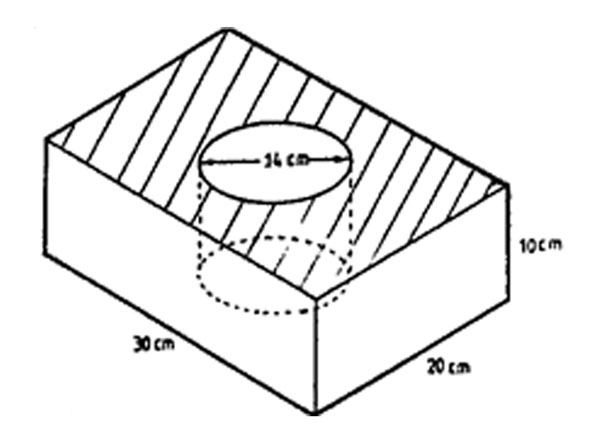
The measurements of the block are 30 cm by 20 cm by 10 cm. The diameter of the hollow cylindrical space is 14 cm. What is the volume of the block? (Take 22/7)
A. 7540 cm3 B. 6000 cm3 C. 4460 cm3 D. 1540 cm3
4. The figure below represents a solid. What is the volume in cm3?
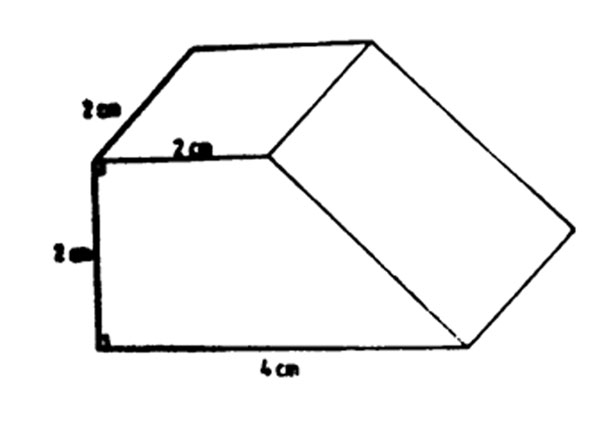
A. 16 B. 32 C. 12 C. 8
5. The figure below shows a metal cylinder with a square hole of side 5 cm made through its length. The diameter of the cylinder is 14 cm and its height 10 cm.
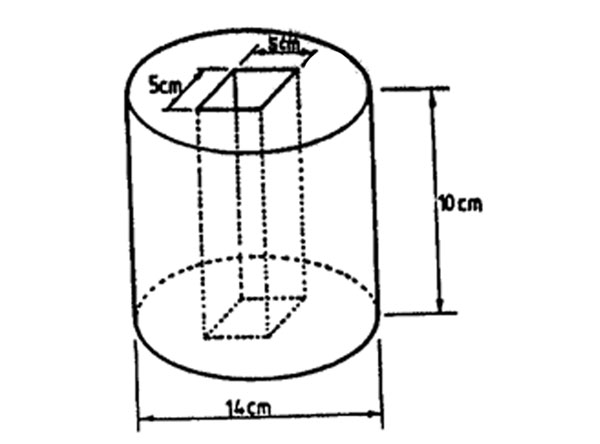
What is the volume of the solid? (Take 22/7)
A. 1540 cm3 B. 1290 cm3 C. 1790 cm3 D. 5910 cm3
6. The diagram below represents a solid made up of a triangular prism from which half a cylinder of diameter 2.8 cm has been removed.
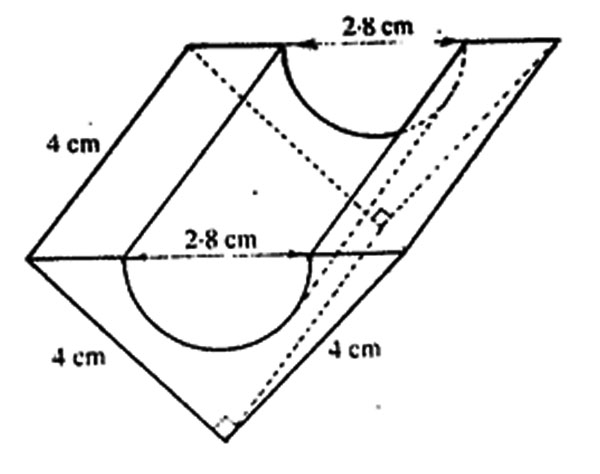
What is the volume of the solid? (Take 22/7)
A. 12.32 cm3 B. 19.68 cm3 C. 32.00 cm3 D. 7.36 cm3
7. The diagram below shows an open rectangular box made of timber. The external measurements of the box are 30 cm, 25 cm, and 15 cm. The thickness of the timber is 2 cm.
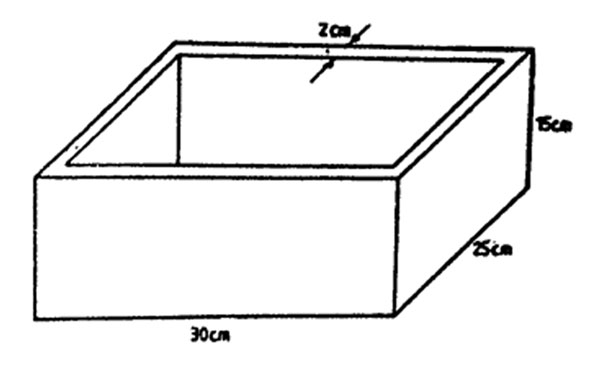
What is the volume of the timber used to make the box?
A. 4152 cm3 B. 2879 cm3 C. 7098 cm3 D. 11250 cm3
8. The figure below represents a solid object in the form of a rectangular block with a semi-circular groove.
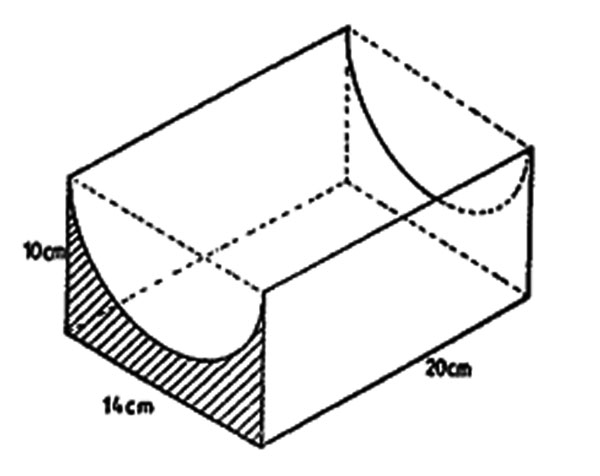
What is the volume of the solid in cm3? (Take 22/7)
A. 1260 cm3 B. 1540 cm3 C. 2360 cm3 D. 2800 cm3
9. The diagram below represents a rectangular solid from which a cylinder of diameter 4.2 cm has been removed.
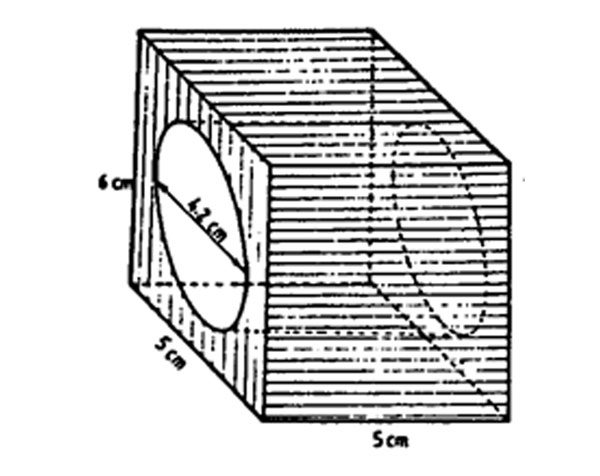
What is the volume of the solid in cm3? (Take 22/7)
A. 150 B. 69.3 C. 84 D. 80.7
10. A cylinder has a height of 12 cm. What is its diameter if its volume is 1848 cm3? (Take 22/7)
A. 154 cm B. 49 cm C. 14 cm D. 7 cm
11. The diagram below represents a solid object. The corners are right-angled and the dimensions are in centimeters.
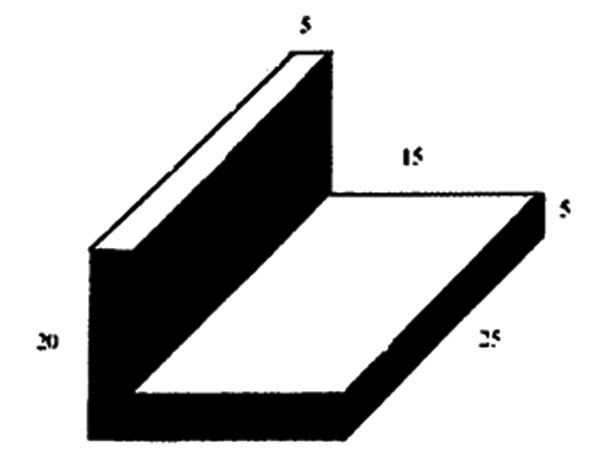
What is the volume of the solid in cm3?
A. 2500 B. 3750 C. 4375 D. 5000
12. A rectangular container whose base measures 70 cm by 60 cm is 35 cm high. If the container is filled with water to a height of 22 cm, what is the volume of the remaining empty space?
A. 147000 cm3 B. 92400 cm3 C. 54600 cm3 D. 100800 cm3
Class 8
1. How many more cubes are needed to fill the box?
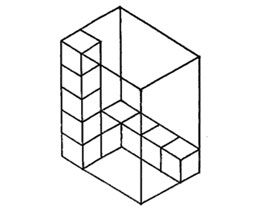
A. 48 B. 60 C. 10 D. 50
2. How many more cubes are needed to fill the box?
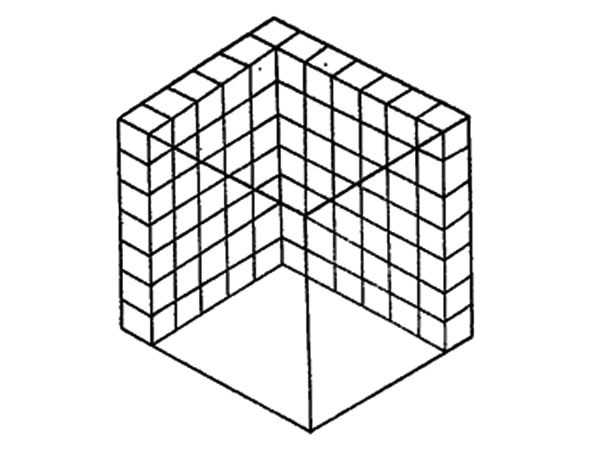
A. 294 B. 210 C. 203 D. 217
3. How many cubes of the same size are arranged in the heap below?
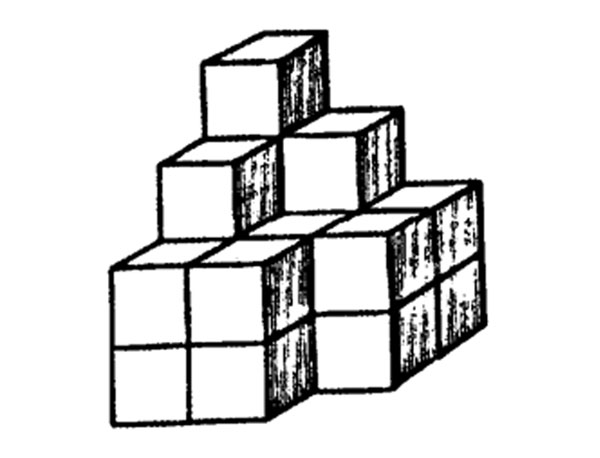
A. 9 B. 11 C. 16 D. 20
4. How many blocks are used to make the pile shown in the figure below?
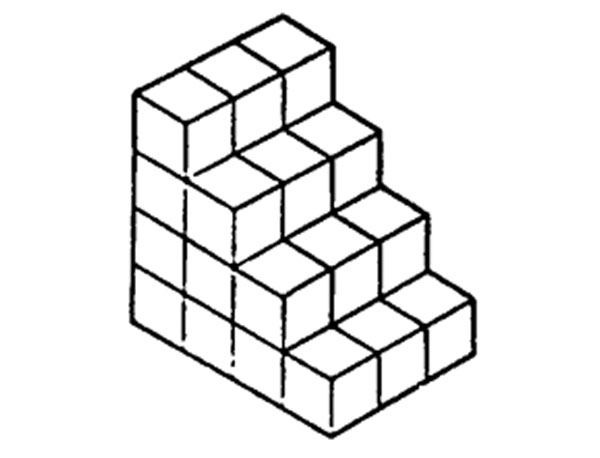
A. 10 B. 24 C. 18 D. 30
5. How many blocks are used to make the pie shown in the figure below?

A. 36 B. 48 C. 60 D. 63
6. How many blocks are used to make the pile shown in the figure below?
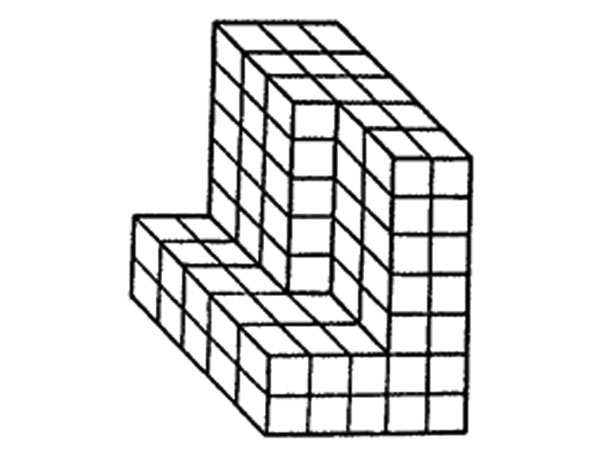
A. 89 B. 115 C. 60 D. 175
7. How many blocks are used to make the pile shown in the diagram below?

A. 70 B. 84 C. 100 D. 175
8. How many cubes if the same size are needed to build the stack below?
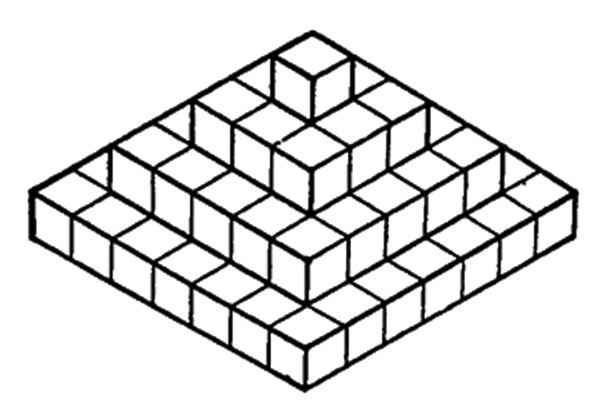
A. 31 B. 49 C. 66 D. 84
9. The figure below represents a stack of cubes. The surface of the stack excluding the base was painted.

How many cubes were painted on two faces only?
A. 10 B. 8 C. 6 D. 4
10. The diagram shows a stack of one-centimetre cubes.
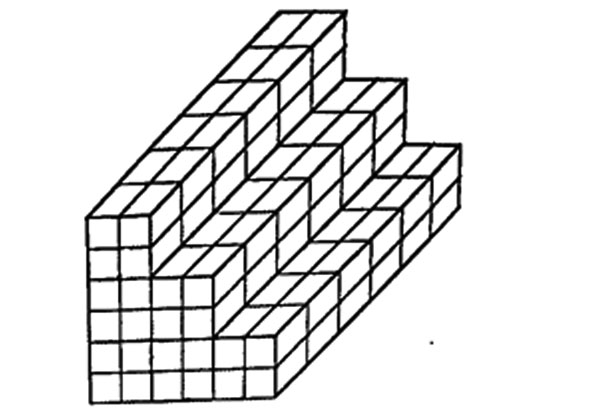
How many more one-centimetre cubes are needed to complete the stack to form a cube of side 6 centimetres?
A. 216 B. 144 C. 96 D. 72
Class 8
1. A rectangular tank of height 2.5 m has a base measuring 1.5 m by 2.0 m. this tank was full of water. After a day’s use, the level of the water fell to 2.1 m. How many litres of water were used? (1 m3 = 1000 litres)
A. 1200 B. 6300 C. 7500 D. 1200000
2. Fifty half-litre packets were repacked into 2-decilitre packets. How many 2-decilitre packets were used?
A. 100 B. 125 C. 25 D. 250
3. The internal measurements of a rectangular tank are length 0.6 m, width 0.5 m, height 0.4 m. How many litres of water are required to fill the tank?
A. 120 B. 1200 C. 12000 D. 120000
4. A cylindrical tank whose internal diameter is 140 cm contains 1155 litres of water. What is the height of the water in the tank? (Take π = and 1 litre = 1000 cm3)
A. 75.0 cm B. 18.75 cm C. 2625.0 cm D. 0.075 cm
5. A cylindrical container has a diameter of 20 cm and is 12 cm high. It contains orange juice up to a height of 5 cm. water is added to fill the container completely. How many cubic centimetres of water is added? (Take π = 3.14)
A. 1570 B. 2198 C. 3768 D. 8792
6. A rectangular container has a square base of side 60 cm. Its height is 90 cm. How many litres of water does it hold when full?
A. 0.324 B. 324 C. 3240 D. 324000
7. A cylindrical container of internal diameter 28 cm is full of water. The height of the water is 30 cm. How many litres of water is this? (Take 22/7)
A. 1.848 B. 18.48 C. 1848 D. 184.8
8. A cylindrical rank of diameter 5.6 m contains 73.92 m3 of water. What is the depth of the water in the tank? (Take )
A. 0.75 m B. 3.0 m C. 0.3 m D. 4.2 m
9. A school received 128 litres of milk packed into 2-deciliter packets. If the packets were in crates each holding 32 packets, how many crates were received?
A. 20 B. 8 C. 4 B. 2
10. A rectangular container holds 5 litres of liquid when full. The base of the container is 40 cm long and 20 cm wide. What is the height of the container in centimeters?
A. 0.625 B. 6.25 C. 62.5 D. 625
11. Wanja had 8 cylindrical containers, each of base area 616 cm2 and height 33 cm. She used the water to fill an empty rectangular tank of volume 162000 cm3. How many litres of water remained when the tank was full?
A. 162.64 l B. 162 l C. 624 l D. 0.624 l
12. A rectangular tank of base 5 m long and 4 m wide has water 2 m deep. How many litres of water are in the tank?
A. 40 l B. 400 l C. 4000 l D. 40000 l
13. A cylindrical tank has an internal radius 1.4 m and height 5 m as shown in the diagram below.
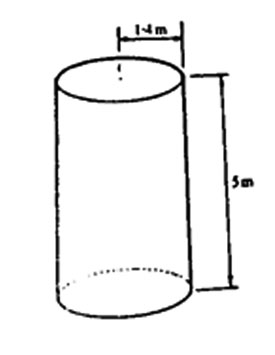
What is the capacity of the tank in litres? (Take )
A. 30800 l B. 3080 l C. 308 l D. 30.8 l
14. A cylindrical container of radius 70 cm is 200 cm deep. The container is filled with water to a depth of 140 cm. What is the volume of water, in cubic metres, needed to fill the remaining part of the container? (Take )
A. 0.0264 m3 B. 0.924 m3 C. 2.156 m3 D. 3.08 m3
15. A cylindrical tank has internal measurements of height 2 m and diameter of 2.8 m. What is the capacity of the tank in litres? (Take )
A. 49280 B. 12320 C. 176 D. 12.32
16. A rectangular container measures 50 cm by 60 cm by 80 cm. How many decilitres of water does it hold when full?
A. 240 B. 2400 C. 24000 D. 240000