| Area |
|---|
| Assessment Questions |
When we refer to a solid such as a cube, the amount of surface is called its surface area.
Area is usually measured in the following units:
If 1 m = 100 cm then
1m² = 1m x 1 m
therefore 1m² = 100 cm x 100 cm
= 10 000 cm²
The following shows how the units of area are related.
We can use the relationships given above to work out the area of specific and combined shapes.
Similarly, we can work out the surface area of solids such as cubes, cuboids, and cylinders.
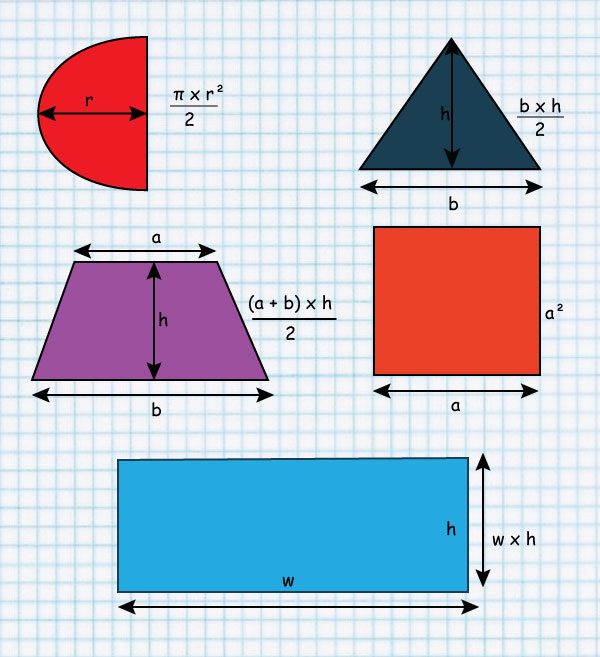
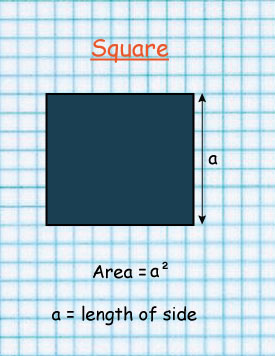
Square
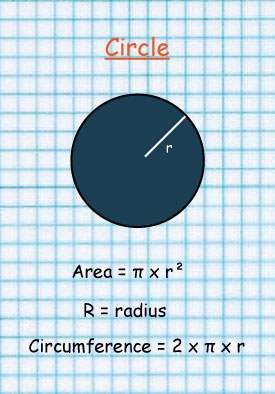
Circle
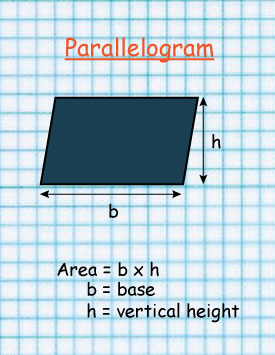
Parallelogram
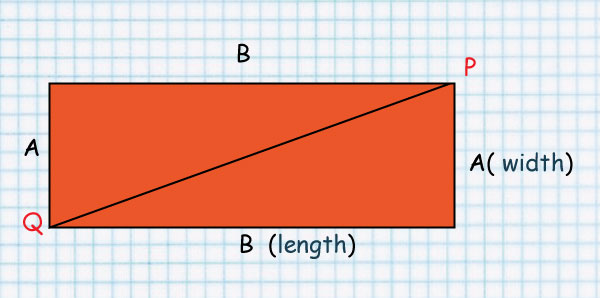
Look at line QP.
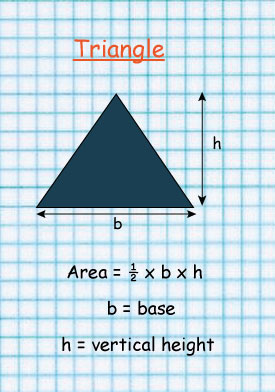
It splits the rectangle into two equal Triangles
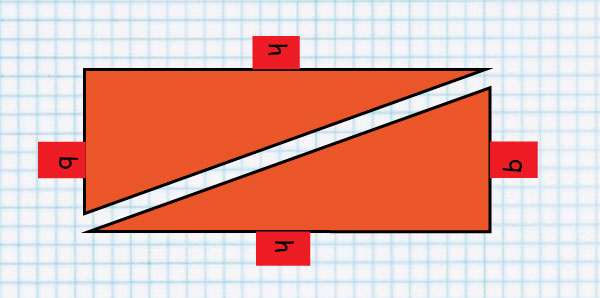
That’s why the Area of a Triangle is 1/2 b x h
Area of a circle is given by:
A = π × r × r
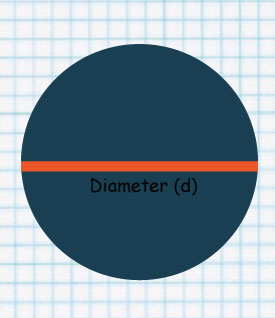
The line at the center is called Diameter.
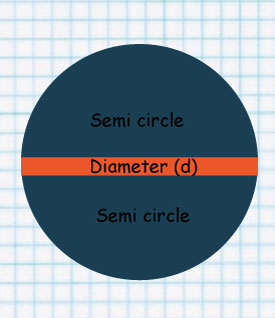
Diameter cuts the circle into two equal parts.
Each part is called semi circle.
A semi-circle can be divided into two equal parts to form a Quadrant
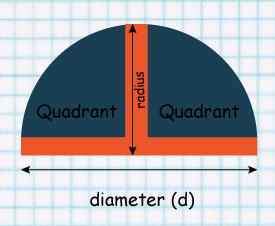
When diameter is divided into 2, a Radius is formed.
Below is a song that teaches you more about circles.
Calculate the area of the circles below
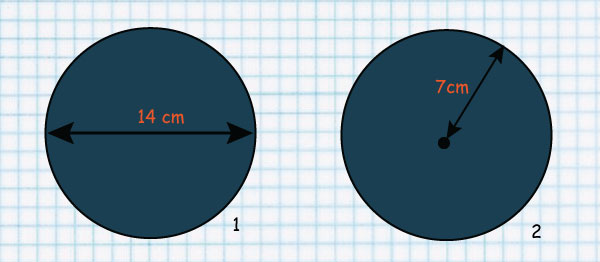
Area of a circle 1 =Pie × r × r
Pie =`22/7`
= × `14/2` cm ×`14/2` cm
=`22/7` × 7cm × 7cm
=22 × 7cm × 1cm
=154cm2
Area of a circle 2 = Pie × r × r
Pie =`22/7`
= `22/7 ` × `14/2` cm × `14/2` cm
=`22/7` × 7cm × 7cm
=22 × 7cm × 1cm
=154cm2
The two circle have the same areas.
The first circle has a diameter of 14cm while the second has a radius of 7cm hence a diameter of 14cm
Find the areas of the shaded part of the circle below given that it has a radius of 7cm.
Solution
Area of the whole circle
=`22/7` × 7cm × 7cm
=22 × 1cm × 7cm
= 154cm2
However the circle has been divided into 4 equal parts each called a Quadrant
To get areas of the shaded part divide 154cm2 by 4
= `154/4` cm2
=38.5cm2
The above parallelogram is made up of two right angled triangles and a rectangle.
The two opposite sides are equal
b=b
a=a
The area of a parallelogram is given by:
Base length × height
Find the area of the shaded regions in the figures below
Area of a parallelogram = base length X height
a ) b)
=9cm × 5cm =10cm × 4cm
= 45 cm squared = 40 cm squared
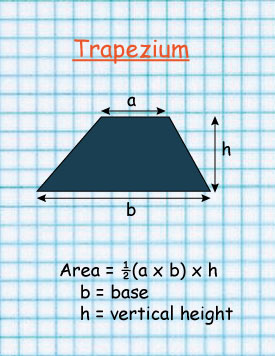
The above trapezium is made up of a rectangle and a right angled triangle.
The area of a Trapezium is given by:
½ h × sum of the two parallel sides(a+b)
Study the image below:
What is the area of the shaded region?
Remember
The area of a Trapezium is given by:
½ h × sum of the two parallel sides(a+b)
½ × 4m × (6m + 8m)
2m × (14m)
=28 metres squared.
1. The area of the figure below is 360m2.
Find the length of a.
2. The figure below represents a plot of land. What is the area of the plot.
1. 60 m
2. 9000 metres squared
The figure below shows a circle of radius 7cm touching the vertices of a square.
What is the area of the shaded part?
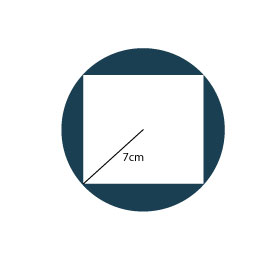
Get the area of the circle A = π r^2
= 3.14 × 7 cm × 7 cm
= 153.86 cm squared
Get the area of the square. The radius gives half the length of the side of the square.
To get full length= 7cm × 2
=14cm
Area of a square =S × S
=14cm × 14cm
=196cm squared
Area of the shaded part = Area of the circle - Area of the square
= 196cm squared- 153.86cm squared
= 42.14cm squared
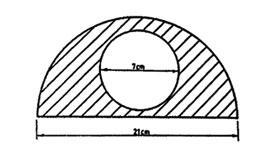
Find the area of the shaded part in the figure below
Take pie = 3.14
The shaded part is made up of a semicircle and a right angled triangle
Area of the semicircle = (πr^2)/2
80cm = diameter
radius =80/2
= 40cm
3.14 x 40cm x 40cm
=5024 cm2/2
=2512cm squared
Area of the triangle = ½ b x h
= ½ x 100cm x 80cm
=50cm x 80cm
= 4000cm squared
Area of the shaded part = 2512cm squared+ 4000cm squared
= 6512cm squared
The image shows a window of a building in Nairobi.
Calculate the area of the window.
Area = area of the rectangle + area of the semicircle
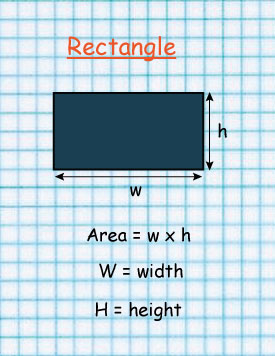
Area of rectangle= l × w
14 m×7 m
=98m2
Area of the semicircle = (πr^2)/2
22/7 ×7 m×7 m
= 154 m2/2
=77 m2
Answer = 98 m2 + 77 m2
=175 m2
Class 7
1. The perimeter of a rectangular field is 14 m. if one of the sides is 3 m, what is the area of the field?
A. 21 m2 B. 33 m2 C. 42 m2 D. 12 m2
2. A circular cut-out of diameter 14 cm is removed from a square board of length 30 cm. What is the area of the piece of board that remains? (Take 22/7)
A. 856 cm2 B. 154 cm2 C. 746 cm2 D. 284 cm2
3. The figure below shows a square WXYZ drawn inside a circle centre O. The radius of the circle is 3.5 cm.
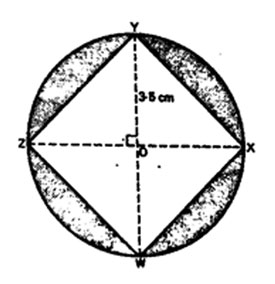
What is the area of the shaded part? (Take 22/7)
A. 38.5 cm2 B. 26.25cm2 C. 24.5 cm2 D. 14.0 cm2
4. What is the area of the shaded region in the diagram below? (Take 22/7)
A. 269.5 cm2 B. 211.75 cm2 C. 173.25 cm2 D. 134.75 cm2
5. The diagram below shows Kamau’s plot of land. The dimensions are as shown in the diagram.
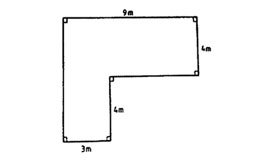
What is the area of the plot?
A. 60 m2 B. 34 m2 C. 72 m2 D. 48 m2
6. What is the area of the shaded part in the figure below?
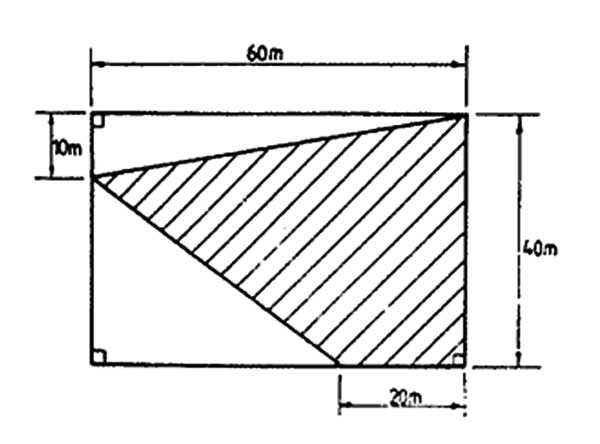
A. 1200 m2 B. 1500 m2 C. 2400 m2 D. 900 m2
7. What is the area of the figure given below?
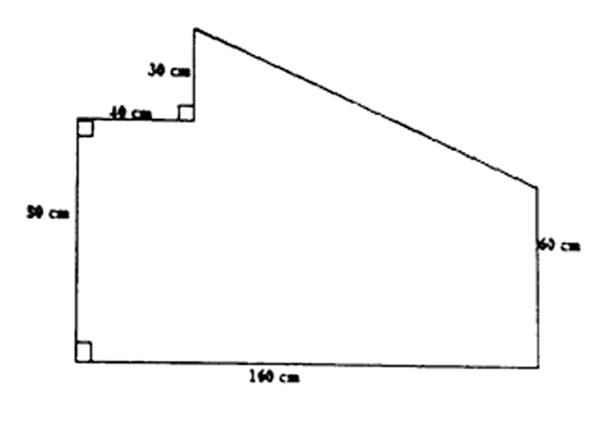
A. 13400 cm2 B. 16400 cm2 C. 12200 cm2 D. 23600 cm2
8. The figure below represents a plot bound by two straight edges and a semi-circle.
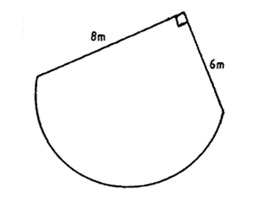
What is the area of the plot? (Take 22/7)
A. 102.550 m2 B. 63.275 m2 C. 39.710 m2 D. 39.275 m2
9. The figure below represents a circle inscribed in a square of side 14 cm.
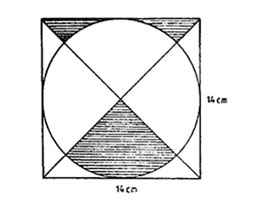
What is the area of the shaded part in cm2? (Take 22/7)
A. 10.5 B. 38.5 C. 42.0 D. 49.0
10. The figure below represents a square enclosed in a circle of radius 7 cm.
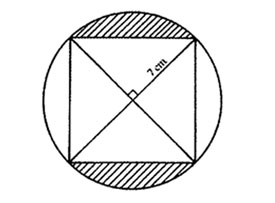
What is the area of the shaded parts? (Take 22/7)
A. 28 cm2 B. 56 cm2 C. 98 cm2 D. 154 cm2
11. In the figure below, XY, YZ, and XZ are diameters of circles.
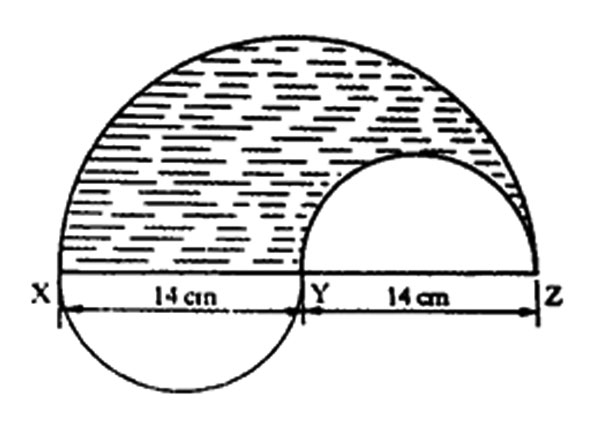
What is the area of the shaded part? (Take 22/7)
A. 462 cm2 B. 385 cm2 C. 308 cm2 D. 231 cm2
12. The shaded part in the figure below represents Kamau’s plot of land.
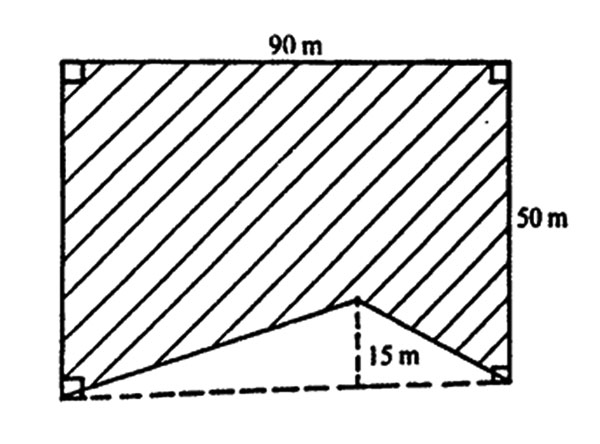
What is the area of the plot in hectares?
A. 0.0675 B. 0.3150 C. 0.4500 D. 0.3825
13. In the diagram below, AB is the diameter of a semi-circle. AB = 10 cm, AC = 8 cm, BC = 6 cm and angle ACB = 900.
What is the area of the shaded part? (Take 22/7)
A. 54.50 cm2 B. 39.25 cm2 C. 24.00 cm2 D. 15.25 cm2
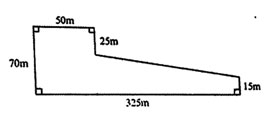
14. The diagram below represents Mwau’s shamba. What is the size of Mwau’s shamba in hectares?
A. 1.175 ha B. 1.325 ha C. 2.0 ha D. 11.75 ha